CRITIKAL BOOK REPORT Tentang MEKANIKA FLUIDA dan TERMODINAMIKA

Oleh:

HERYADIK SIMATUPANG

NIM:5132131004

Jurusan pendidikan teknik elektro

$D:\Foto\Logo UNIMED.jpg$

UNIVERSITAS NEGERI MEDAN

2013

KATA PENGANTAR

Puji dan syukur saya panjatkan kepada Tuhan Yang Maha esa atas segala kasih dan pertolangan-Nya saya dapat meyelesaikan Book Report ini.

Adapun karya ini dimaksudkan untuk memberi manfaat bagi para pembaca untuk memahami perbandingan tentang Mekanika Fluida maupun Termodinamika antara satu buku/satu sumber dengan buku/sumber yang lainnya.

Saya menyadari bahwa makalah ini masih terdapat banyak kekurangan dan saya mengharapkan kritik dan saran yang bersifat membangun dari setiap pembaca demi kesempurnaan karya ini.Semoga makalah ini dapat bermanfaat bagi kita semua.

Medan,…November 2013

Penulis

………………………………….

HERYADIK SIMATUPANG

NIM :5132131004

Pendahuluan

A.Latar Belakang

Seiring dengan perkembangan ilmu pengetahuan,makin besar pula keinginan setiap orang untuk terus berpacu dalam dunia pendidikan yaitu belajar.

Membuat Book Report adalah salah satu metode pembelajaran yang sangat penting karna memberi pemahaman didalam membandingkan suatu buku dengan buku yang lainnya.

Karya ini hadir sebagai bahan pembelajaran dan media baca dengan harapan agar setiap pembaca akan mendapatkan manfaat akibat efek membaca dari karya ini.

B.Rumusan Masalah

Berdasarkan latar belakang diatas,yang menjadi rumusan masalah dalam Book Report ini adalah Mekanika Fluida dan Termodinamika 1 dan 2.

C.Tujuan

Adapun tujuan penulisan Book Report ini yaitu untuk memahami perbandingan tentang Mekanika Fluida maupun tentang Termodinamika 1 dan 2 dari dua buku yang berbeda dan setiap pembaca dapat menarik kesimpulan dari masing-masing buku yang dibandingkan.

BAB 1.RINGKASAN MATERI

A. MEKANIKA FLUIDA (BUKU 1)

A. Pengertian Fluida

Fluida adalah zat – zat yang berubah bentuk secara kontinyu atau terus menerus bilaterkena tegangan geser, berapapun kecilnya tegangan geser itu. (Ł)

Dimana :

Tegangan Geser (Ł) = F dimana F = Gaya geser

A = Luas Permukaan

Fluida terdiri dari 2 macam yaitu ; zat cair dan zat gas :

a) Zat Cair (liquid)

Zat Cair tidak mudah dimampatkan (Incompressible)

b) Zat Gas

Gas mudah dimampatkan (Compressible)

B. Satuan Gaya, Massa, Panjang, dan Waktu

Terdapat dua sistim satuan yang biasa dipakai

1. Sistim Internasional

2. Sistim British (digunakan di USA, Inggris)

a. Satuan Internasional

Gaya F N Newton

Massa m Kg Kilogram

Panjang (long) l m Meter

Waktu (time) t s Second (detik)

Sesuai dengan hukum newton II, tentang gerakan

F= m.a a = percepatan = - m/s2

N = Kg. m/s2 jadi 1 N = 1 Kg m/s2

b. Satuan British (USA)

Gaya F lb Pound

Massa m Slug

Panjang l ft(foot) fett(kaki)

Waktu t s Second (detik)

Jadi 1 lb = 1 Slug FtS-2

Tetapi ada pula yang menggunakan :

Gaya (lb), massa (lbm), panjang (ft), dan waktu (s) sehingga diperlukan keseimbangan.

dalam hukum newton:

F : M x ag

g : gaya grafotasi

g = 32,174 fts-2

nilai g untuk sistem satuan

Sistem	Massa	Panjang	Waktu	Gaya	g
SI	Kg	m	S	N	1 Kgm/n2
British	Slug	Ft	S	Lb	1 sluf ft/lbs2
British	Lbm	Ft	S	Lb	#2,174 lbm ft/lbs2
Metrik, Cgs	G	Cm	S	Dyn	19 cm/dyn.s2
Metrik, Mks	Kg	M	S	Kgf	9,81 kgm/kgfs2

Ba (m) tidak berubah dengan lokasinya, yang berubah adalah beratnya (W) sesuai dengan kecepatan grafitasinya (g) Jadi :

W = m.g

Contoh :

1. Suatu benda berat 1 lb pada g = 32,174 ft/s2 berat benda pada g = 31,5 ft/s2

Jawab =

m (massa) = Wg = 1032,174

jadi = W pada g = 31,5 ft/s2 W = m.g

W = 1032,174 x 31,5

= 9, 79 lb

2. Suatu benda dengan massa (m) = 10 kg, hitunglah berat benda bila g = 9,81m/s2

Jawab : W = m.g

= 10 kg x 9,81 m/s2

= 98,1 kgm/s2

= 98,1 N

C. Viskositas

Viskositas adalah kekentalan, viskositas sangat mempengaruhi sifat – sifat fluida. Contoh benda yang di viskos (kental) adalah madu, sirup, aspal cair. Sedangkan fluida yang viskositasnya kecil adalah air, alcohol, udara. Fluida yang viskositasnya kecil lebih mudah mengalir bila dibandingkan dengan fluida yang viskositasnya besar. Viskositas dengan gas meningkat dengan naik temperature, tetapi mudah cairan sebaliknya viskositas menurun gas, naiknya temperature akan terjadi perpindahan molekul – molekul yang padat, cair, naiknya temperature akan menutunkan kohesi. Efek viskositas pada gerakan

A = luas Plate (luas penampang)

V = kecepatan plate atas, relative terhadap plate bawah

Y = tebal lapisan cairan

F = t x A tegangan geser x luas permukaan

t x A =μ Vy .A jadi : t = μ Vy .A

Dimana :

t = teggangan geser

μ = viskositas mutlak (Viskositas Dinamik)

satuan μ N.s/m2 atau kg/m.s2

yang lazim digunakan adalah poise (P) 1 Poise = 1 dyn.s cm2

Viskositas kinetic (n )

n = μρ ρ = density (rapat massa)

n = m/s2, cm/s2

Satuan yang lazim digunakan adalah Stoke

1 stoke = 1 cm/s2

D. Keratapan volume jenis, berat jenis, gravitasi jenis, tekanan.

➢ Keratapan = massa jenis = rapat jenis = density

Adalah perbandingan antara massa (m) dan volume (v)

Density ρ = mV =Kgm3

Untuk air pada 760 mm Hg dan 4o C, ρ = 1000 kg/m3 = 1 ton/m3

➢ Volume jenis atau volume spesifik (Vs)

Adalah kebalikan dari density (ρ) , yaitu volume yang ditempati

massa satuan fluida.

Jadi : Vs = 1/ ρ atau V/m m3/kg

➢ Berat jenis akan spesifik

Adalah berat zat persatuan volume

= ρ.g = kg/m3 x m/s2 = N/m3

Berat spesifikasi akan berubah sesuai dengan lokasinya.

Bila g diabaikan = ρ........kg/m3

➢ Gravitasi jenis atau spesifik gravitasi (s)

Adalah perbandingan antara berat spesifik fluida dengan spesifik

air pada temperature 4o C dan volume yang sama.

Jadi : s = berat spesifik fluida Berat spesifikasi air 4°C non dimensi

E. TEKANAN (press (p))

Adalah gaya normal yang mendorong bidang datar dibagi dengan luas bidang itu.

Untuk tekanan, biasa dinyatakan dengan tinggi kolam fluida.

P = g .h h = tinggi kolam cairan (fluida)

= N x mm3

= Nm2 (Pa)

P = ρ.g.h Kgm3 x ms2 m = Nm2

Contoh soal :

bila tekanan 1 atm dan di ukur dengan ekivalen ketinggian kolam air, hitung fungsi kolam air tersebut :

Jawab :

p = 1 atm = 105 N m3 , ρ air = 1000 N m3

g = 9,81 m/s2

P = .h

P = ρ.g.h h = PP.g

h = 1000001000 x 9,81

h = 10,2 m

jadi setiap ketinggian 10,2 m kolam air setara dengan 1 atm (1kg/cm2).

10,2 m diameter tidak mempengaruhi

P = 1 atm

B.TERMODINAMIKA

1. Keadaan dan Sifat Termodinamika

Keadaan suatu system tertutup yang berada dalam kesetimbangan (equilibrium) merupakan kondisi yang ditentukan berdasarkan nilai dari sifat termodinamikanya. Berdasarkan pengamatan berbagai system termodinamika diketahui bahwa tidak semua sifat bebas satu dengan lainnya, dan secara khusus suatu keadaan dapat ditentukan berdasarkan nilai sifat bebasanya. Nilai dari sifat termodinamika lainnya ditentukan dari bagian bebas ini. Aturan umum yang dikenal sebagai prinsip keadaan telah dikembangkan sebagai arahan dalam menentukan jumlah sifat bebas yang diperlukan untuk menetapkan keadaan suatu system.

Prinsip keadaan menegaskan bahwa tekana, energi dalam spesifik, dan sifat intensif lainnya yang terkait dapat ditentukan sebagai fungsi dari T dan ; dan sebagainya. Hubungan fungsional dapat dikembangkan menggunakan data eksperimental dan bergantung secara eksplisit pada identitas sifat kimia zat penyusun system.

Evaluasi Tekanan, Volume Spesifik, dan Temperatur

Tabel Cair dan Uap

Sifat uap air diberikan pada Tabel A-4, sedangkan untuk cairan air pada Tabel A-5. Tabel ini sering disebut sebagai Tabel uap panas lanjut dan Tabel cairan tekan. Tabel A-4 dan A-5 disusun untuk memberikan nilai beberapa sifat sebagai fungsi dari tekanan dan temperature. Sifat pertama yang terdapat dalam tabel adalah volume spesifik.

Untuk setiap nilai tekanan yang terdapat dalam tabel uap panas lanjut (Tabel A-4), diawali dengan keadaan uap jenuh dan kemudian ke temperature yang lebih tinggi. Dalam Tabel cairan tekan (Tabel A-5) berakhir dengan keadaan cair jenuh. Ketika menyelesaikan soal, keadaan yang didapati sering tidak tepat pada titik nilai yang tersedia pada tabel sifat. Sehingga, perlu dilakukan interpolasi dengan teliti terhadap nilai-nilai entri yang berdekatan dalam tabel sifat.

Tabel Jenuh

Tabel uap jenuh (saturation table), Tabel A-2 dan A-3 memberikan nilai sifat untuk keadaan cair jenuh dan keadaan uap jenuh, yang ditandai oleh subskrip f dan g. Tabel A-2 disebut tabel temperature, karena temperature disusub dalam kolom pertama dengan peningkatan tertentu. Kolom kedua menampilkan tekanan terkait. Dua kolom berikutnya masing-masing memberikan nilai volume spesifik cairan jenuh , dan volume spesifik uap jenuh

Tabel A-3 disebut tabel tekanan, karena tekanan disusun dalam kolom pertama dengan peningkatan tertentu. Dua kolom berikutnya masing-masing memberikan nilai .Untuk suatu campuran dua fase cair dan uap, rasio massa uap terhadap massa total campuran merupakan kualitas campuran, x, yang dapat dihitung sebagai berikut

Volume spesifik campuran dua fase cair-uap dapat ditentukan menggunakan tabel jenuh dan definisi kualitas sesuai Persamaan (3.1) sebagai berikut.

Kualitas didefinisikan sebagai, dan perhatikan bahwa sehingga apabila disubtitusikan ke persamaan di atas, akan diperoleh

Evaluasi Energi Dalam dan Entalpi Spesifik

Dalam banyak analisis termodinamika, sering didapati penjumlahan energi dalam U dan perkalian anatar tekanan p dengan volume V. Karena penjumlahan sering muncul, maka untuk memudahkan diperkenalkan nistilah yang disebut entalpi yang diberi lambing H. Sesuai definisi

Karena U, p, dan V adalah sifat, maka kombinasinya juga suatu sifat. Entalpi persatuan massa didefinisikan sebagai

Data energi dalam spesifik u dan entalpi h diperoleh dari tabel sifat dengan cara yang sama seperti pada volume spesifik. Untuk keadaan jenuh, nilai uf dan ug, serta hf dan hg, ditabulasi terhadap tekanan dan temperature jenuh. Energi dalam spesifik untuk campuran dua fase cair-uap untuk nilai kualitas tertentu, dihitung dengan cara yang sama dengan perhitungan volume spesifik, yaitu

Evaluasi Kalor Spesifik CV dan CP

Berbagai sifat penting dalam termodinamika berkaitan dengan energi dalam. Salah satunya adalah entalpi yang telah diperkenalkan sebelumnya. Pada subbab ini akan dibahas dua sifat lainnya, yang dikenal sebagai kalor spesifik (specific heats). Kalor spesifik sangat penting khususnya untuk perhitungan termodinamika model gas ideal.

Definisi sifat intensif cv dan cp untuk zat murni kompresibel sederhan, sebagai fungsi dari turunan parsial dan , masing-masing sebagai

Evaluasi Sifat Zat Cair dan Padat

Perkiraan sifat cairan menggunakan data cairan jenuh

Perkiraan nilai v, u, dan h pada keadaan cair dapat diperoleh menggunakan data cair jenuh. Sebagai gambaran perhatikanlah tabel cair tekan, Tabel A-5. Tabel ini memperlihatkan bahwa pada suatu temperature tetap, volume spesifik dan energi dalam spesifik hanya sedkiti dipengaruhi oleh adanya perubahan tekanan. Karena nilai v dan u hanya sedikit berubah, saat tekanan berubah pada temperature tetap, maka perkiraan berikut memadai untuk dipergunakan dalam perhitungan teknik:

Suatu perkiraan nilai h pada keadaan cair dapat diperoleh menggunakan Persamaan (3.12) dan (3.13) sesuai definisi

Persamaan ini dapat dituliskan dalam bentuk alternative sebagai

dengan psat adalah tekanan jenuh (saturasi) pada temperature tertentu. Jika komponen Persamaan (3.14) yang ditandai garis bawah memberikan kontribusi yang kecil, entalpi spesifik dapat diperkirakan menggunakan nilai cair jenuh, seperti hanya untuk v dan u. Jadi,

Model zat inkompresibel

Sesuai pembahasan di atas, terdapat daerah di mana volume spesifik cairan air relative tetap dan energi dalam spesifik berubah sesuai perubahan temperature. Perilaku umum yang sama juga diperlihatkan oleh beberapa zat dalam cairan dan oleh zat padat. Berdasarkan pengamatan ini, dapat dilakukan perkiraan menggunakan Persamaan (3.12) sampai (3.15), maupun menggunakan model zat inkompresibel (incompressible substance model).

Untuk menyederhanakan evaluasi yang melibatkan zat cair atau zat padat, volume spesifik (densitas) diasumsikan tetap dan energi dalam spesifik diasumsikan hanya berubah sesuai perubahan temperature. Suatu zat yang diidealisasikan seperti ini disebut zat inkompresibel

1. Air dalam bejana adalah system tertutup.

2. Keadaan 1, 2, dan 3 adalah keadaan kesetimbangan.

3. Volume bejana tetap konstan.

Analisi: Dua sifat bebas diperlukan untuk menetapkan keadaan 1 dan 2. Pada keadaan awal, tekanan dan kualitas diketahui. Karena keduanya bersifat bebas, maka keadaannya telah tertentu. Keadaan 1 ditunjukkan pada diagram T-v dalam daerah dua fase. Volume spesifik pada keadaan 1 diperoleh mempergunakan nilai kualitas yang diberikan serta Persamaan (3.2), yaitu

Pada keadaan 2, tekanan diketahui. Sifat lain yang diperlukan untuk menetapkan keadaan adalah volume spesifik . Volume dan massa tetap, sehingga m3/kg. Untuk p2 = 1,5 bar, Tabel A-3 memebrikan dan . Karena , keadaan 2 juga harus berada di dalam daerah dua fase cair-uap. Keadaan 2 juga ditunjukkan pada diagram T-v di atas.

a) Karena keadaan 1 dan 2 berada di dalam daerah dua fase cair-uap, temperature yang berkaitan dengan temperature jenuh untuk tekanan yang diberikan. Tabel A-3 memberikan

T1 = 99,63oC dan T2 = 111,4oC

b) Untuk mendapatkan massa uap air yang ada, digunakan volume dan volume spesifik untuk mendapatkan massa total m, yaitu

Kemudian berdasarkan Persamaan (3.1) dan nilai kualitas yang diberikan, massa uap pada keadaan 1 adalah

Dengan cara yang sama, massa uap pada keadaan 2 diperoleh menggunakan nilai kualitas x2. Untuk menyelesaikan x2, selesaikanlah Persamaan (3.2) untuk kualitas dan masukkan data volume spesifik dari Tabel A-3 pada tekanan 1,5 bar, beserta dengan nilai yang diketahui, sebagai berikut

Kedumidan, berdasarkan persamaan (3.1), maka

c) Jika pemanasan dilanjutkan, keadaan 3 akan berada pada garis uap jenuh, seperti ditunjukkan pada diagram T-v di atas. Jadi, tekanan merupakan tekanan jenuh terkait. Karena pada Tabel A-3,

= 0,8475 m3/kg berada diantara va = 0,8857 m3/kg pada pa = 2,0 bar dan vb = 0,7187 m3/kg pada pb = 2,5 bar, maka interpolasi tekanan terkait p3 adalah

Contoh 3.2. Air yang berada dalam system silinder-torak mengalami dua proses berseri dari suatu keadaan awal yang mempunyai tekanan 10 bar dan temperature 400oC. Porses 1-2: Air didinginkan saat dikompresi pada tekanan tetap 10 bar ke keadaan uap jenuh. Proses 2-3: Air didinginkan pada volume tetap ke 150oC. a) Tentukanlah kerja untuk seluruh proses (kJ/kg), b) Tentukanlah perpindahan kalor untuk seluruh proses (kJ/kg).

Penyelesaian

Diketahui: Air yang berada dalam system silinder-torak mengalami dua proses. Didinginkan dan dikompresi pada tekanan tetap, dan didinginkan pada volume tetap.

Ditanyakan: Tentukan kerja neto dan perpindahan kalor neto untuk seluruh proses persatuan massa yang berada dalam system silinder-torak.

Asumsi:

1. Air dalam silinder-torak merupakan system tertutup.

2. Kerja hanya terjadi pada torak.

3. Tidak terjadi perubahan energi kinetic dan potensial.

a) Karena mekanisme kerja hanya terjadi pada torak, maka

Integral kedua dapat dihilangkan untuk Proses 2-3 karena berlangsung pada volume tetap. Persamaan di atas dibagi dengan massa dan disederhanakan untuk tekanan.

Volume spesifik keadaan 1 diperoleh dari Tabel A-4 menggunakan p1 = 10 bar dan T1 = 400oC: = 0,3066 m3/kg. Juga = 2957,3 kJ/kg. Volume spesifik pada keadaan 2 adalah nilai uap jenuh pada 10 bar, dari Tabel A-3, diperoleh = 0,1944 m3/kg. Jadi kerja keseluruhan proses adalah

Tanda minus menunjukkan bahwa kerja diberikan pada uap air oleh torak

b) Neraca energi untuk keseluruhan proses dapat disederhanakan menjadi

Untuk menghitung perpindahan kalor diperlukan u3, yaitu energi dalam spesifik pada keadaan 3. Karena T3 tersedia dan v3 = v2, maka dua sifat intensif bebas telah diketahui dan dapat digunakan untuk menetapkan keadaan 3. Untuk mendapatkan u3, pertama-tama dihitung nilai kualitas.

3.2.Grafik Kompresibilitas Umum

Tujuan subbab ini adalah untuk mendapatkan pemahaman yang lebih baik mengenai hubungan tekanan, volume spesifik, dan temperature gas. Hal ini penting bukan hanya sebagai dasar analisis gas, tetapi juga untuk pembahasan di mana model gas ideal diperkenalkan. Subbab ini membahas factor kompresibilitas, yang diawali dengan memperkenalkan konstanta gas universal.

Konstanta Gas Universal

Anggaplah suatu gas berada di dalam system silinder-torak yang dijaga pada temperature tetap. Torak dapat digerakkan bebas, sehingga berbagai keadaan kesetimbangan pada temperature tetap dapat dicapai. Misalkan tekanan dan volume spesifik diukur pada setiap keadaan, dan nilai perbandingan (adalah volume per mol) dapat ditentukan. Selanjutnya dapat dibuat grafik rasio tersebut terhadap tekanan pada temperature tetap. Hasil untuk beberapa temperature diperlihatkan pada Gambar 3-3.

Jika rasio tersebut diekstrapolasi ke tekanan nol, suatu nilai batas yang tepat sama dapat diperoleh untuk setiap kurva. Jadi,

dengan adalah batasan umum untuk semua temperature. Jika prosedur ini diulang untuk gas-gas yang lain, maka dapat diperoleh bahwa batas rasio ketika p mendekati nol pada temperature tetap adalah sama, yaitu . Karena selalu diperoleh niali yang sama besar untuk semua gas, maka nilai disebut sebagai konstanta gas universal. Nilai yang ditentukan secara eksperimental

Faktor Kompresibilitas

Rasio tak berdimensi disebut sebagai factor kompresibilitas dan diberi lambing Z.

Seperti digambarkan pada perhitungan berikut, jika nilai dan T digunakan dengan satuan yang konstan, maka Z tak berdimensi.

Karena dengan M adalah berat atom atau berat moleku, factor kompresibilitas dapat dituliskan dalam bentuk alternative sebagai

R adalah sebuah konstanta untuk gas tertentu yang mempunyai berat molekul M. Satuan alternative untuk R adalah kJ/kg.K, Btu/lb.oR, dan ft.lbf/lb.oR.

Jadi, factor kompresibilitas Z cenderung bernilai satu saat tekanan mendekati nol pada temperature tertentu. Hal ini dapat dilihat pada Gambar 3-4, yang memperlihatkan grafik Z hydrogen terhadap tekanan pada berbagai temperature.

Gambar 3-4 memperlihatkan factor kompresibilitas hydrogen terhadap tekanan pada nilai temperature tertentu. Grafik sejenis untuk berbagai gas lain juga tersedia, dan apabila diamatai grafik-grafik tersebut tampak serupa secara kualitatif. Dengan melakukan penyesuaian koordinat, kurva dari berbagai jenis gas yang digambarkan pada sumbu koordinat yang sama, akan saling berdekatan, sehingga menunjukkan adanya kesrupaan kualitatif. Kondisi seperti ini disebut sebagai prinsip keterkaitan keadaan (principle of corresponding states). Dalam pendekatan semacam ini, factor kompresibilitas Z, digambarkan terhadap tekanan yang diturunkan pR dan temperature yang diturunkan TR tak berdimensi, yang didefinisikan sebagai

dengan pc dan Tc adalah tekanan dan temperature kritis. Sebagai hasilnya didapat grafik kompresibilitas umum (generalized compressible chart) dalam bentuk . Gambar 3-5 memperlihatkan data eksperimental untuk 10 gas berbeda pada grafik semacam ini. Garis tebal adalah garis isothermal yang diturunkan, yang merupakan regresi terbaik dari data eksperimental.

3.3.Model Gas Ideal dan Proses Politropik Gas Ideal

3.3.1. Model Gas Ideal

Pembahasan sebelumnya menunjukkkan bahwa secara umum hubungan antara temperature, tekanan, dan volume spesifik gas cukup rumit. Subbab 3.2 telah memperlihatkan bahwa pada keadaan di mana p relative kecil terhadap tekanan kritis pc (pR rendah) dan atau temperature T realtif besar terhadap temperature kritis Tc (TR tinggi), maka factor kompresibilitas mendekati nilai satu. Pada keadaan semacam ini, dapat diasumsikan bahwa Z = 1,

3.3.2.Proses Politropik Gas Ideal

Proses politropik system tertutup dapat diuraikan menggunkan hubungan tekanan-volume dalam bentuk

dengan n adalah konstanta (sudah diperkenalkan dalam subbab 2.2). Untuk proses politropik di antara dua keadaan atau

Pangkat eksponen n dapat berupa sebuah nilai antara dan , bergantung pada prosesnya. Ketika n = 0, proses adalah proses isobaric (tekanan tetap), dan ketika , proses adalah proses isometric (volume tetap).

Untuk proses politropik

untuk semua nilai eksponen n kecuali n = 1. Ketika n = 1

3.4.Energi Dalam, Entalpi dan Kalor Spesifik Gas Ideal

Karena gas mengikuti model gas ideal, energi dalam spesifik bergantung hanya pada temperature. Jadi, kalor spesifik cv, seperti didefinisikan Persamaan (3.9), juga hanya sebagai fungsi temperature

Dengan cara yang sama, karena gas mengikuti model gas ideal, entalpi spesifik juga hanya bergantung pada temperature, sehingga kalor spesifik cp, seperti didefinisikan Persamaan (3.10), juga hanya sebagai fungsi temperature.

Tabulasi data kalor spesifik untuk gas tertentu diberikan sebagai fungsi temperature dalam Tabel A-20. Kalor spesifik juga tersedia dalam bentuk persamaan. Beberapa bentuk alternative persamaan tersebut jumpai dalam literature teknik. Persamaan alternative yang mudah diintegralkan adalah dalam bentuk polynomial

Nilai konstanta dan untuk beberap gas tersedia dalam Tabel A-21, untuk kisaran temperature 300 sampai dengan 1000 K (540 sampai dengan 1800oR).

C.TERMODINAMIKA 2

1. Ketidaksamaan Clausius

Ketidaksamaan Clausius mendasari dua hal yang digunakan untuk menganalisis system tertutup dan volume atur berdasarkan hukum kedua termodinamika, yaitu sifat entropi dan neraca entropi. Ketidaksamaan Clausius menyatakan bahwa:

di mana mewakili perpindahan kalor pada batas system selama terjadinya siklus, dan T adalah temperature absolute pada daerah batas tersebut. Subskrip “b” menunjukkan bahwa integral dihitung pada daerah batas yang mengalami siklus.

. Ilustrasi yang digunakan untuk mengembangkan ketidaksamaan Clausius

memperlihatkan sebuah system untuk mendapatkan energi sebesar di daerah batas dengan temperature absolute T pada saat system menghasilkan kerja . Berdasarkan definisi skala Kelvin (Persamaan 5.6) diperoleh hubungan antara perpindahan kalor dan temperatur seperti:

Selanjutnya, perhatikan gabungan system seperti pada Gambar 6.1 yang ditunjukkan oleh garis putus-putus. Neraca energi pada kombinasi tersebut di mana adalah kerja total dari kombinasi system, penjumlahan antara dan menyatakan perubahan energi dari kombinasi system tersebut. Penyelesaian persamaan neraca energi untuk dengan mengganti dengan Persamaan (6.1a) didapat:

Bila system tersebut di biarkanlah menjalani siklus tunggal, sementara system antara menjalani siklus satu kali atau lebih. Kerja total dari kombinasi system gabungan tersebut adalah

Karena kombinasi system tersebut menjalani siklus dan memindahkan energi dengan perpindahan kalor pada sebuah reservoir kalor, Persamaan 5.1 memenuhi pernyataan Kelvin-Planck tentang hukum kedua termodinamika. Berdasarkan hal ini, Persamaan (6.1b) disederhanakan hingga didapat Persamaan 6.1, di mana kesamaan dapat digunakan, pada saat tidak terdapat ireversibilitas dalam system yang melakukan siklus. Ketidaksamaan diaplikasikan jika terdapat ireversibilitas internal. Pengertian ini sebenarnya berkaitan dengan adanya kombinasi system dan siklus antara. Namun, pada siklus antara tersebut dapat dianggap tidak terjadi ireversibilitas, jadi kemungkinan terjadinya ireversibilitas adalah pada system itu sendiri

2. Perubahan Entropi Pada Gas Idean dan Zat Inkompresibel

2.1.Pengertian Perubahan Entropi

Suatu besaran adalah sebuah sifat jika dan hanya jika perubahan nilai yang terjadi di antara dua keadaan tidak tergantung pada proses. Aspek konsep sifat ini digunakan bersama dengan Persamaan 6.2 dalam pembahasan mengenai entrpi.

Gambar 6-2 memperlihatkan dua buah siklus yang dihasilkan oleh sebuah system tertutup. Siklus pertama terdiri dari sebuah proses reversible internal A dari keadaan 1 ke keadaan 2, yang diikuti oleh proses reversible internal C dari keadaan 2 ke keadaan 1. Siklus yang lain terdiri dari sebuah proses reversible internal B dari keadaan 1 ke keadaan 2, yang diikuti oleh proses reversible internal C dari keadaan 2 ke keadaan 1

Pada kedua Persamaan 6.3 tersebut, sama dengan nol karena siklus tersebut disusun dari proses reversible internal. Dengan mensubtitusikan Persamaan 6.3b ke dalam Persamaan 6.3a, di dapat.

Dengan menggunakan symbol S yang menunjukkan suatu sifat yang disebut entropi, maka perubahannya dapat ditulis sebagai berikut:

di mana subskrip, “int rev” diberikan untuk mengingatkan bahwa integrasi tersebut dilakukan untuk setiap proses reversible internal yang menghubungkan dua keadaan. Persamaan 6.4a merupakan definisi dari perubahan entropi. Dalam bentuk diferensial, persamaan di atas dapat dituliskan

Entropi merupakan sifat ekstensi. Satuan SI untuk entropi spesifik adalah kJ/kg.K untuk s dan kJ/kmol.K untuk . Sedangkan Satuan Inggris untuk entropi spesifik adalah Btu/lboR dan Btu/lbmoloR.

2.2. Perubahan Entropi Gas Ideal

Persamaan T dS dibentuk dengan memperhitungkan system kompresibel sederhana, dan murni, yang menggunakan proses reversible internal. Persamaan diferensial neraca energi tanpa memperhitungkan pergerakan system secara keseluruhan dan adanya gravitasi adalah

Sesuai definisi system kompresibel sederhana, maka kerja menjadi

Persamaan 6.4b disusun kembali, untuk mendapatkan perpindahan kalor yang terjadi sebagai

Subtitusi Persamaan 6.6 ke dalam Persamaan 6.5 di dapat persamaan T dS pertama:

T dS = dU + p dV Persamaan T dS kedua, dikembangkan dari Persamaan 6.7 menggunakan H = U + pV. Dalam bentuk persamaan diferensial, diperoleh:

dH = dU + d(pV) = dU + p dV + V dp

Setelah disusun ulang menjadi

dU + p dV = dH – V dp

Subtitusikan Persamaan di atas ke dalam Persamaan 6.7, didapat persamaan T dS kedua:

T dS = dH – V dp (6.8)

Persamaan T dS dapat dalam basis satuan massa, sebagai:

T ds = du + p dv (6.9a)

T ds = dh – v dp (6.9b)

Persamaan T dS digunakan untuk mendapatkan besarnya perubahan entropi antara dua keadaan gas ideal. Kita mulai dengan Persamaan 6.9

Karena R konstan, suku terakhir dari Persamaan 6.11 dapat langsung diintegrasikan. Namun karena cv dan cp merupakan fungsi temperature untuk gas ideal, penting untuk mendapatkan informasi tentang hubungan fungsional sebelum integrasi suku terakhir dari persamaan ini dilakukan

Seperti halnya untuk perubahan energi dalam dan entalpi, perhitungan perubahan entropi untuk gas ideal dapat dipermudah dengan pendekatan table. Untuk melakukan ini, pertam tentukanlah keadaan referensi dan nilai acuan: Nilai entropi spesifik ditentukan sama dengan nol, pada temperature 0 K dan tekanan 1 atm. Kemudian, dengan menggunakan Persamaan 6.12b, entropi spesifik pada keadaan referensi, dengan temperature T dan tekanan 1 atm, ditentukan relative terhadap keadaan dan nilai acuan.

Simbol melambangkan entropi spesifik pada temperature T dan tekanan 1 atm. Karena hanya tergantung temperature, maka nilai tersebut dapat ditabulasi terhadap temperature, seperti halnya pada h, dan u. Untuk udara sebagai gas ideal, dengan satuan kJ/kg.K atau Btu/lb.oR diberikan pada Tabel A-22. Nilai untuk beberapa gas diberikan pada Tabel A-23 dengan satuan kJ/kmol.K atau Btu/lb mol.oR. Karena integral Persamaan 6.12b dapat dimasukkan ke dalam bentuk

Dari persamaan di atas, maka Persamaan 6.12b dapat dituliskan menjadi

Karena kalor spesifik cp dan cv konstan, maka perubahan entropi gas ideal dalam persamaan 6.12a dan 6.12b dapat disederhanakan menjadi

2.3. Perubahan Entropi Pada Zat Inkompresibel

Model zat inkompresibel yang diperkenalkan pada Subbab 3.1 mengasumsikan bahwa volume spesifiknya (densitasnya) konstan dan kalor spesifik hanya bergantung pada temperature, cv = c(T). Maka perubahan diferensial energi dalam spesifik adalah du = c(T) dT dan Persamaan 6.10, menjadi:

Setelah diintegrasik, perubahan entropi spesifik Jika kalor spesifik dianggap konstan.

Penyelesaian

6.3. Perubahan Entropi Dalam Proses Reversibel Internal

Ketika system tertutup mengalami suatu proses reversible internal, entropi system dapat meningkat, menurun, atau tetap tidak berubah. Hal ini dapat dijelaskan dengan Persaman 6.4b:

yang mengindikasikan bahwa pada saat system tertutup mengalami proses reversible internal, menerima energi melalui perpindahan kalor, system tersebut mengalami peningkatan entropi. Sebaliknya, ketika energi dikurangi dari system tersebut oleh perpindahan kalor, entropi system menurun. Hal ini dapat diartikan bahwa perpindahan entropi menyertai perpindahan kalor, dengan arah perpindahan keduanya sama. Dalam proses adiabatic reversible internal, entropi memiliki kecenderungan untuk konstan. Proses entropi konstan dinamakan proses isentropic.

Dari Persamaan 6.20 dapat disimpulkan bahwa perpindahan energi oleh kalor pada system tertutup selama proses reversible internal dapat diwakili oleh luasan pada diagram temperature entropi. Gambar 6-3 menunjukkan luasan yang mewakili besarnya perpindahan kalor yang terjadi selama proses reversible internal dengan variasi temperature.

Untuk menunjukkan hubungan antara perubahan entropi yang menyertai dengan perpindahan kalor dan luasan grafik, perhatikan gambar 6-4a, yang menunjukkan suatu siklus daya Carnot (Subbab 5.5).

Siklus yang diperlihatkan pada gambar 6-4a terdiri dari 4 proses reversible internal; dua proses isothermal dan dua proses adiabatic. Pada proses 2-3 adalah proses isotermal, perpindahan kalor pada system muncul pada saat temperature system konstan pada TH, maka entropi system akan meningkat karena adanya perpindahan entropi. Dengan menggunakan Persamaan 6.20, maka proses ini memberikan jadi luasan 2-3-a-b-2 pada Gambar 6-3a mewakili perpindahan kalor yang terjadi selama proses. Proses 3-4 adalah proses adiabatic dan reversible internal sehingga sama dengan proses isentropic (entropi-konstan). Proses 4-1 adalah proses isothermal pada temperature TC di mana kalor keluar dari system. Karena perpindahan entropi terjadi bersama dengan perpindahan kalor, maka entropi system menurun. Untuk proses ini, Persamaan 6.4, merumuskan menjadi yang mempunyai nilai negative. Area 4-1-b-a-4 pada Gambar 6-3a menunjukkan besarnya perpindahan kalor Q41. Proses 1-2 yang melengkapi siklus, adalah proses adiabatic dan reversible internal (isentropic). Jadi kerja neto suatu siklus sama dengan perpindahan kalor neto, yang terjadi pada siklus tersebut. Dengan demikian, luasan tertutup 1-2-3-4-1 menunjukkan kerja neto siklus.

Jika siklus ini diterapkan pada Gambar 6-4b, maka akan menghasilkan siklus Carnot untuk refrijerasi atau pompa kalor. Pada siklus semacam ini, perpindahan kalor ke system terjadi pada saat temperature konstan TC, jadi entropi meningkat pada proses 1-2. Dalam proses 3-4 kalor keluar dari system pada temperature konstan sebesar TH, sehingga entropi menurun.

4.Neraca Entropi Untuk System Tertutup Dan Volume Atur

4.1. Neraca Entropi Untuk Sistem Tertutup

Perumusan Neraca Entropi

Gambar 6-6. Siklus yang digunakan dalam merumuskan neraca entropi

Gambar 6-6 memperlihatkan siklus yang dilakukan oleh sebuah system tertutup. Siklus terdiri dari Proses I, di mana terjadi ireversibilitas internal, diikuti dengan proses reversible internal R.

di mana integral pertama untuk proses I, dan integral kedua untuk proses R. Subskrib “b” menandakan bahwa integral pertama dihitung pada batas system. Subskrip tidak diperlukan untuk integral kedua, karena temperature system merata di setiap bagian, pada setiap keadaan antara proses reversible internal. Karena tidk terdapat ireversibilitas yang berhubungan dengan proses R, suku

pada Persamaan 6.2, yang menandakan efek ireversibilitas selama siklus, hanya dapat diterapkan pada proses I, seperti diperlihatkan pada Persamaan 6.20 sebagai

Dengan menerapkan definisi perubahan entropi, kita dapat merumuskan integral kedua dari Persamaan 6.20 sebagai:

Sehingga Persamaan 6.20 menjadi

Akhirnya, dengan menyusun kembali persamaan terkahir, diperoleh neraca entropi system tertutup, menjadi

Terminologi pertama dari Persamaan 6.21 sebelah kanan menggambarkan perpindahan kalor dari atau menuju system selama proses. Terminologi ini dapat diartikan sebagai perpindahan entropi menyertai perpindahan kalaor. Aarah perpindahan enetropi sama dengan perpindahan kalor dan tanda yang digunakan sama, yaitu positif jika entropi masuk ke system, dan negative jika entropi keluar dari system.

Perubahan entropi system tidak hanya tergantung pada perpindahan entropi, tetapi juga bergantung pada suku kedua di bagian kanan Persamaan 6.21 yang dinyatakan dengan Terminologi bernilai positif jika terjadi ireversibilitas internal selama proses, nol jika tidak terjadi ireversibilitas internal. Hal ini dapat dikatakan bahwa entropi diproduksi di dalam system karena adanya kegiatan ireversibilitas internal selama berlangsungnya proses. Hukum kedua termodinamika dapat diartikan sebagai kebutuhan produksi entropi terhadap proses ireversibilitas internal dan dipertahankan hanya dengan mengurangi ireversibilitas sampai mendekati nol.

Ketika neraca entropi diterapkan pada system tertutup, maka perlu diperhatikan syarat-syarat yang dikenakan oleh hukum kedua termodinamika terhadap nilai produksi entropi: Hukum kedua mempersyaratkan bahwa nilau produksi entropi adalah positif atau nol

Produksi entropi tidak mungkin bernilai negative. Namun, perubahan entropi system dapat bernilai positif, nol, dan negative.

Neraca Entropi Sistem Tertutup

Neraca entropi dapat dinyatakan dalam berbagai bentuk yang mungkin sesuai untuk analisis tertentu. Contohnya, jika perpindahan kalor terjadi pada beberap lokasi di batas system, dengan temperature tidak bervariasi terhadap lokasi atau waktu, bentuk perpindahan entropi yang terjadi di mana Qj/Tj adalah jumlah perpindahan entropi melalui bagian batas pada temperature an penjumlahan.

Berdasarkan basis laju waktu, maka neraca laju entropi pada system tertutup, adalah dengan dS/dt adalah laju waktu perubahan entropi. Suku Qj/Tj mewakili laju perpindahan entropi pada batas system dengan temperature sesaat Tj. Suku merupakan laju waktu produksi entropi selama terjadinya ireversibilitas di dalam system. Terkadang lebih mudah untuk menuliskan neraca entropi dalam bentuk diferensial

1. Pada bagian (a), kotak transmisi dianggap sebagai system tertutup pada keadaan tunak, seperti pada gambar di atas dengan menggunakan data dari contoh 2.3.

2. Pada bagian (b), kotak transmisi dan suatu bagian dari lingkungan sekitarnya dianggap sebagai system tertutup, seperti pada gambar di atas dengan menggunakan data dari contoh 2.3.

3. Temperatur permukaan terluar kotak transmisi dan temperature disekitarnya adalah sama.

Prinsip Peningkatan Entropi

Pembahasan ini difokuskan pada system yang diperluas sebagai sebuah system dan bagian lingkungan yang terpengaruh pada saat berlangsungnya proses. Karena semua energi dan perpindahan massa terjadi di dalam batas system yang telah diperluas, maka system yang diperluas dapat dianggap sebagai system yang terisolasi. Neraca energi untuk system .

karena tidak terdapat perpindahan energi melewati batas system. Jadi, energi system terisolasi adalah tetap. Karena energi merupakan sifat ekstensif, nilai energi untuk system terisolasi adalah penjumlahan besarnya energi system dan sekeliling (soundarings).

Dari kedua persamaan ini, prinsip kekekalan energi memberikan batas terhadap proses yang mungkin muncul. Untuk terjadinya suatu proses, sangat penting agar energi system ditambah dengan lingkungan tetap konstan. Namun, tidak setiap proses yang memenuhi batasan tersebut dapat terjadi. Proses tersebut harus memenuhi hukum kedua termodinamika.

di mana adalah jumlah total dari produksi entropi yang dihasilkan oleh system dan lingkungannya. Karena produksi entropi terjadi pada semua proses actual, maka proses yang dapat terjadi adalah proses yang meningkatkan jumlah entropi pada system yang terisolasi. Hal ini dikenal sebagai prinsip peningkatan entropi.

Karena entropi merupakan sifat ekstensif, maka nilai entropi untuk system tertutup adalah jumlah total dari produksi entropi yang dihasilkan oleh system dan lingkungannya.

4.2. Laju Neraca Entropi Dalam Volume Atur

Seperti halnya massa dan energi, entropi merupakan sifat ekstensi, jadi entropi juga dapat ditransfer dari atau ke dalam persamaan volume atur oleh aliran material. Karena hal ini merupakan perbedaan mendasar antara bentuk system tertutup dan volume atur, maka nereca laju entropi volume atur (control volume entropy rate balance) dapat dicapai dengan memodifikasi Persamaan 6.28 dengan memperhitungkan perpindahan entropi. Hasilnya adalah

di mana dScv/dt adalah laju waktu perubahan entropi dalam volume atur. Suku dan merupakan laju perpindahan entropi yang terjadi ke atau dari volume atur yang menyertai perpindahan massa. Pada penulisan Persamaan 6.34, diasumsikan terjadinya aliran satu dimensi pada lokasi di mana massa masuk dan keluar. Suku Qj menunjukkan laju waktu perpindahan kalor pada lokasi di daerah batas system dengan temperature Tj. Rasio Qj/Tj menunjukkan laju perpindahan entropi. Suku mewakili laju produksi entropi per satuan waktu selama terjadinya ireversibilitas pada volume atur.

Analisis Volume Atur Pada Keadaan Tunak

Analisis dengan menggunakan volume atur pada keadaan tunak banyak digunakan dalam analisis teknik. Karena itu penting untuk memahami bentuk keadaan tunak neraca massa, energi, dan entropi. Pada keadaan tunak, prinsip kekekalan massa Dan neraca laju entropi pada keadaan tudak diperoleh dengan menyederhanakan Persamaan 6.34, sebagai

Volume Atur Satu Masukkan Satu Keluaran

Karena banyak aplikasi merupakan volume atur pada keadaan tunak dengan satu-aliran masuk dan satu-aliran keluar, bentuk persamaan neraca laju entropi untuk permasalahan ini sangat penting.

Atau, jika dibagi dengan aliran massa persamaan di atas menjadi

Dua suku disebelah kanan Persamaan 6.36 menunjukkan besarnya laju perpindahan entropi yang bersama dengan perpindahan kalor ke dalam volume atur, dan besarnya laju produksi yang dihasilkan volume atur, keduanya per satuan massa yang mengalir melalui volume atur. Pada kasus khusus di mana tidak ada perpindahan entropi bersamaan dengan perpindahan kalor,

5.Poses Isentropik

Hal-Hal Umum Yang Harus Diperhatikan

Sifat-sifat pada tiap-tiap keadaan yang memiliki entropi spesifik yang sama dapat dihubungkan dengan menggunakan grafik dan table data. Sebagai contoh, seperti ditunjukkan pada Gambar 6-11 yang memperlihatkan diagram temperature-entropi dan entalpi-entropi sangat membantu dalam menentukan sifat pada keadaan-keadaan yang memiliki nilai entropi spesifik yang sama. Semua keadaan pada garis vertical yang melalui satu keadaan tertentu memiliki nilai entropi yang sama. Nilai-nilai dari beberapa sifat-sifat yang lain pada keadaan 2 dan 3 dapat dibaca kemudian secara langsung dari gambar-gambar.

Untuk contoh kasus pada Gambar 6-11, entropi spesifik pada keadaan 1 dapat ditentukan dari table uap panas lanjut. Kemudian, dengan s2 = s1 dan satu nilai sifat lain, seperti p2 dan T2, keadaan 2 dapat ditentukan letaknya pada table uap panas lanjut. Nilai-nilai sifat-sifat, v, u,dan h pada keadaan 2 dapat ditentukan dari table.

Perhatikan bahwa keadaan 3 jatuh pada daerah dua fase cair-uap pada Gambar 6-11. Karena s3 = s1, kualitas pada keadaan 3 dapat ditentukan menggunakan persamaan:

Kualitas campuran x dapat dihitung dari energi dalam spesifik dengan persamaan

Penggunaan Model Gas Ideal

Gambar 6-12. Dua keadaan gas ideal di mana s2 = s1

Gambar 6-12 memperlihatkan dua keadaan gas ideal yang memiliki nilai entropi spesifik yang sama. Dengan mempertimbangkan hubungan antara tekanan, volume spesifik, dan temperature pada keadaan ini, pertama menggunakan table gas ideal dan kemudian mengasumsikan kalor spesifik adalah tetap. Dari dua keadaan yang memiliki entropi spesifik yang sama, Persamaan 6.14a direduksi menjadi

Persamaan 6.14a mempergunakan empat nilai sifat: p1, T1, p2, dan T2. Jika terdapat tiga sifat yang diketahui, maka yang keempat dapat diketahui. Sebagai contoh, jika temperature pada keadaan 1 dan perbandingan p2/p1 diketahui, maka temperature pada keadaan 2 dapat diketahui dari

Karena T1 diketahui, dapat diketahui dari table yang cocok, nilai dari dapat dihitung, dan temperature T2 dapat diketahui dari interpolasi. Jika p1, T1, dan T2 diketahui dan tekanan pada keadaan 2 dicari, Persamaan 6.41a dapat digunakan untuk mendapatkan

Persamaan 6.41 dapat digunakan ketika data atau diketahui, dan Tabel gas A-22 dan A-23.

Untuk jenis kasus khusus di mana udara dimisalkan sebagai gas ideal, Persamaan 6.41c dapat digunakan sebagai dasar untuk alternative pendekatan table yang menghubungkan temperature dan tekanan pada dua keadaan yang memiliki entropi spesifik yang sama. Untuk itu persamaannya dapat diubah menjadi

Nilai yang muncul pada persamaan ini murni sebagai fungsi dari temperature, dan ditulis dengan symbol pr(T). Tabulasi dari pr terhadap temperature untuk udara terdapat pada Tabel A-22. Dalam fungsi pr, persamaan menjadi

(s1 = s2, hanya udara (6.42)

di mana pr1 = pr(T1) dan pr2 = pr(T2). Fungsi pr terkadang disebut sebagai tekanan relative. Kita dapat juga mengembangkan hubungan antara volume spesifik dan temperature untuk dua keadaan udara yang memiliki entropi spesifik sama. Dengan persamaan gas ideal, v = RT/p, perbandingan volume spesifik adalah

Karena kedua keadaan memiliki entropi spesifik yang sama, Persamaan 6.42 dapat digunakan untuk mendapatkan

Perbandingan RT/pr(T) yang muncul pada sisi kanan dari persamaan terakhir murni fungsi temperature, dan diberi symbol vr(T). Nilai dari vr ditabulasikan terhadap temperature di dalam modul ini untuk udara pada Tabel A-22. Dalam fungsi vr, persamaan terakhir menjadi

di mana dan . Fungsi vr terkadang disebut volume relative.

6.Efisiensi Isentropic Turbin, Nosel, Kompresor dan Pompa.

Efisiensi Turbin Isentropik

Untuk memahami efisiensi turbin isentropic, lihat Gambar 6-14 yang memperlihatkan ekspansi turbin pada diagram Mollier. Keadaan awal ketika memasuki turbin dan tekanan keluar turbin telah ditentukan. Perpindahan kalor antara turbin dan lingkungan diabaikan, begitupun dengan efek energi kinetic dan potensial. Dengan asumsi-asumsi ini, neraca laju massa dan energi menjadi lebih sederhana, pada keadaan tetap, sehingga kerja per satuan massa yang melewati turbin adalah

Karena keadaan 1 tetap, entalpi spesifik h1 dapat diketahui, sehingga nilai kerja hanya bergantung pada entalpi spesifik h2, dan meningkat dengan penurunan h2. Nilai maksimum untuk kerja turbin didapatkan dari nilai terkecil entalpi spesifik yang diizinkan pada keluaran turbin. Hal ini dapat ditentukan menggunakan hukum kedua. Keadaan keluar yang diizinkan dibatasi oleh

yang dapat diperoleh dengan penuruna laju entropi.

Karena produksi entropi tidak dapat bernilai negative, keadaan dengan tidak diperbolehkan dalam ekspansi adiabatic. Ekspansi sebenarnya hanya dapat dicapai dengan . Keadaan yang ditandai oleh “2s” pada Gambar 6-14 dapat dicapai hanya jika tidak ada ireversibilitas internal. Hal ini disebut dengan ekspansi isentropic pada turbin. Untuk tekanan keluar tetap, entalpi spesifik h2 menurun bersamaan dengan penurunan entropi s2. Nilai terkecil yang diizinkan untuk h2 sama dengan keaadan 2s, dan niali maksimum untuk kerja turbin adalah

Dalam ekspansi nyata pada turbin h2 >h2s, sehingga kerja yang lebih kecil dibandingkan dengan kerja maksimum. Dari perbedaan ini dapat dihitung efisiensi turbin isentropic yang didefinisikan olek

Nilai biasanya berkisar antara 0,7 hingga 0,9 (70 – 90 %).

Efisiensi Nosel Isentropik

Efisiensi nosel isentropic didefinisikan sebagai perbandingan dari energi kinetic spesifik nyata dari gas yang meninggalkan nosel, dengan energi kinetic keluar yang dapat dicapai ekspansi isentropic pada keadaan masuk yang sama dan tekanan keluar yang sama juga

Efisiensi nosel biasanya hingga 95 % atau lebih, menunjukkan bahwa nosel yang dibuat dengan baik memiliki ireversibilitas internal mendekati nol.

Efisiensi Pompa dan Kompresor Isentropik

Bentuk dari efisiensi isentropic untuk kompresor dan pompa dibahas bersama mengacu pada Gambar 6-15, yang menunjukkan proses kompresi pada diagram Mollier. Keadaan saat memasuki kompresor dari tekanan keluar tetap. Dengan perpindahan kalor, energi kinetic, dan energi potensial yang dapat diabaikan, kerja masuk per satuan massa yang mengalir melewati kompresor adalah

Karena keadaan 1 tetap, entalpi spesifik h1 dapat diketahui. Oleh Karena itu, nilai kerja masuk hanya bergantung pada entalpi spesifik h2 pada keluaran. Pernyataan di atas menunjukkan bahwa besar kerja input menurun dengan menurunnya h2. Kerja minimum masuk ialah nilai terkecil yang diperbolehkan untuk entalpi spesifik pada keluaran kompresor. Dengan alasan yang sama untuk turbin, entalpi ini adalah entalpi pada keadaan keluar yang dapat dicapai pada kompresi isentropic dari keadaan masuk dan tekanan keluar tertentu.

6.7.Perpindahan Kalor dan Kerja Dalam Proses Aliran Tunak Reversible Internal

Pembahasan kita pada Subbab ini adalah tentang volume atur dengan satu masukkan (inlet), dan satu keluaran (outlet) pada keadaan tunak. Tujuannya adalah guna memperoleh pernyataan untuk perpindahan kalor dan kerja tanpa adanya ireversibilitas internal.

Perpindahan Kalor

Untuk volume atur pada keadaan tunak di mana alirannya isothermal dan reversible internal, bentuk neraca laju entropi yang tepat adalah

di mana 1 menyatakan inlet dan 2 outlet, adalah aliran laju massa. Dengan menyelesaikan persamaan ini, perpindahan kalor per satuan massa yang melewati volume atur adalah

Secara umum, temperature akan bervariasi ketika gas atau cairan mengalir melewati volume atur. Kemudian, perpindahan kalor per satuan massa dinyatakan sebagai

Subskrip “int rev” digunakan untuk mengingatkan bahwa pernyataan di atas hanya berlaku pada volume atur di mana tidak ada ireversibilitas internal. Integral Persamaan 6.48 bergerak dari inlet ke outlet. Jika keadaan-keadaan yang dilewati satuan massa ketika bergerak dari inlet ke outlet volume atur seperti yang digambarkan oleh diagram T-s, besar perpindahan kalor per satuan massa yang mengalir dapat dinyatakan sebagai daerah di bawah kurva

Kerja

Kerja per satuan massa melewati volume atur dapat ditentukan dari neraca laju energi, yang direduksi pada keadaan tunak menjadi

Persamaan ini adalah pernyataan dari prisip kekekalan energi yang digunakan, baik ketika ada ireversibilitas dalam volume atur maupun tidak. Namun, jika permasalahan dibatasi pada kasus reversible internal, Persamaan 6.48 dapat diubah menjadi

Karena tidak ireversibilitas internal, satu satuan massa melewati serangkaian keadaan kesetimbangan sejak masuk hingga keluar. Perubahan entropi, entalpi, dan tekanan dihubungkan oleh Persamaan 6.9b

T ds = dh – v dp

Jika diintegrasikan menjadi

Dengan hubungan ini, Persamaan 6.49 menjadi

Jika keadaan yang dilewati ketika massa bergerak dari inlet ke outlet volume atur, seperti yang digambarkan oleh diagram p-v pada Gambar 6-18b, besar integral digambarkan oleh daerah yang diarsir di belakang kurva.

Persamaan 6.50a seringkali dipergunakan pada peralatan seperti turbin, kompresor, dan pompa. Dalam banyak kasus seperti ini, tidk ada perubahan energi kinetic dan potensial yang berarti, jadi

Untuk setiap kenaikan tekanan yang sama, pompa akan membutuhkan kerja masukan per satuan massa yang lebih sedikit dibandingkan dengan kompresor, karena volume spesifik cairan yang lebih kecil daripada uap. Kesimpulan ini juga secara kualitatif tepat untuk pompa dan kompresor actual, di mana terdapat ireversibilitas selama operasi.

Persamaan 6.50b seringkali digunakan dalam satu dari beberap bentuk khusus. Sebagai contoh, jika volume spesifik selalu mendekati satu nilai konstan, seperti berbagai aplikasi dengan menggunakan cairan, maka

Persamaan 6.50c dapat juga digunakan untuk mempelajari kinerja volume atur pada keadaan tunak di mana adalah nol, seperti dalam kasus nosel dan diffuser. Untuk semua kasus, persamaan menjadi

yang merupakan bentuk dari persamaan Bernoulli yang seringkali digunakan dalam mekanika fluida.

A.MEKANIKA FLUIDA (BUKU 2)

A. PENGERTIAN FLUIDA

Fluida adalah zat yang dapat mengalir dan memberikan sedikit hambatan terhadap perubahan bentuk ketika ditekan. Fluida terbagi dua yaitu dinamika fluida dan statika fluida. Ilmu mengenai fluida dalam keadaan bergerak disebut sebagai dinamika fluida. Sedangkan,statika fluida juga disebut hidrostatika, yaitu cabang ilmu yang mempelajari fluida dalam keadaan diam. Statika fluida mencakup kajian kondisi fluida dalam keadaan kesetimbangan yang stabil. Penggunaan fluida untuk melakukan kerja disebut hidrolika, Fluida statis selalu mempunyai bentuk yang dapat berubah secara kontinyu mengikuti bentuk wadahnya karena fluida tidak dapat menahan gaya geser

B. TEKANAN STATIK DI DALAM FLUIDA

Karena sifatnya yang tidak dapat dengan mudah dimampatkan, fluida dapat menghasilkan tekanan normal pada semua permukaan yang berkontak dengannya. Pada keadaan diam (statik), tekanan tersebut bersifat isotropik, yaitu bekerja dengan besar yang sama ke segala arah. Karakteristik ini membuat fluida dapat mentransmisikan gaya sepanjang sebuah pipa atau tabung, yaitu, jika sebuah gaya diberlakukan pada fluida dalam sebuah pipa, maka gaya tersebut akan ditransmisikan hingga ujung pipa. Jika terdapat gaya lawan di ujung pipa yang besarnya tidak sama dengan gaya yang ditransmisikan, maka fluida akan bergerak dalam arah yang sesuai dengan arah gaya resultan.

Konsepnya pertama kali diformulasikan, dalam bentuk yang agak luas, oleh matematikawan dan filsuf Perancis, Blaise Pascal pada 1647 yang kemudian dikenal sebagai Hukum Pascal. Hukum ini mempunyai banyak aplikasi penting dalam hidrolika. Galileo Galilei, juga adalah bapak besar dalam hidrostatika.

C. TEKANAN HIDROSTATIK

Sevolume kecil fluida pada kedalaman tertentu dalam sebuah bejana akan memberikan tekanan ke atas untuk mengimbangi berat fluida yang ada di atasnya. Untuk suatu volume yang sangat kecil, tegangan adalah sama di segala arah, dan berat fluida yang ada di atas volume sangat kecil tersebut ekuivalen dengan tekanan yang dirumuskan sebagai berikut

dengan (dalam satuan SI),

P adalah tekanan hidrostatik (dalam pascal);

ρ adalah kerapatan fluida (dalam kilogram per meter kubik);

g adalah percepatan gravitasi (dalam meter per detik kuadrat);

h adalah tinggi kolom fluida (dalam meter).

D.FLUIDA IDEAL

Sebelum kita membahas fluida statis, kita batasi terlebih dahulu fluida yang seperti apa yang akan kita pelajari. Fluida yang akan kita pelajari kali ini adalah fluida idela. Sifat – sifat dari fluida ideal adalah:

1. Incompressible (tidak mengalami perubahan ketika mendapat tekanan)

2. Non viscosity (ketika bergerak tidak mengalami gesekan)

3. Alirannya stasioner (konstan)

E.DEFENISI FLUIDA STATIS

Apakah anda pernah menaruh air dalam gelas. Kemudian air itu didiamkan sampai tidak ada bagian – bagian air yang berpindah (tentunya bagian – bagian yang dimaksud yang bersifat makro). Keadaan seperti itulah yang dinamakan fluida statis, yaitu fluida yang tidak mengalami perpindahan bagian – bagiannya. Pada fluida statis kita akan mempelajari mengenai tekanan dan tegangan permukaan.

Tekanan Hidrostatis

Apabila kita menyelam di danau ataupun di lautan, maka semakin dalam kita menyelam kita akan merasakan adanya tekanan yang semakin besar. Demikian pula tekanan atmosfer akan semakin berkurang dengan bertambahnya ketinggian. Inilah sebabnya kabin pesawat terbang harus diberi tekanan. Namun, untuk atmosfer kita agak susah menentukan tekanannya pada suatu ketinggian tertentu karena kerapatan atmosfer tidak konstan. Untuk cairan seperti air yang kerapatannya konstan, maka tekanan akan bertambah secara linear sesuai dengan bertambahnya kedalaman. (kedalaman dihitung dari permukaan fluida tersebut).

Coba kita perhatikan fluida yang ada dalam gelas! Kita anggap saja fluida tersebut merupakan fluida ideal.

Pada lapisan bagian atas, fluida mendapatkan tekanan atmosfer (Po). Namun, karena fluida memiliki masa maka akan menimbulkan gaya berat yang akan menekan pada dasar gelas tersebut. Sehingga tekanan yang dialami oleh dasar gelas adalah:

Karena tekanan merupakan gaya per satuan luas daerah yang dikenai gaya ( ), maka tekanan pada dasar gelas adalah:

Telah kita ketahui bahwa massa jenis benda itu merupakan massa per satuan volume, sehingga

Kita asumsikan, gelas tersebut merupakan silinder. Sehingga volumenya adalah luas alas dikalikan dengan tingginya (V = A h)

Dengan demikian, tekanan hidrostatis pada dasar gelas adalah:

Ternyata, tekanan hidrostatis bergantung pada kedalaman dan tidak bergantung pada bentuk dan luas permukaan bejana. Sehingga tekanan hidrostatis pada satu jenis fluida pada permukaan bumi akan sama untuk semua titik yang memiliki kedalaman yang sama.

B.TERMODINAMIKA 1

Hukum I termodinamika adalah suatu pernyataan bahwa energi adalah kekal, energi tidak dapat diciptakan / dimusnahkan.

Hukum ini menyatakan, jika kalor ΔQ masuk ke dalam sistem, energi ini haruslah muncul sebagai penambahan energi dalam sistem ΔU dan/atau usaha yang dilakukan sistem pada lingkungannya.

Energi dapat berganti bentuk yang lain, misalnya: menjadi kalor.

1 joule = 0,24 kalori ; 1 kalori = 4,2 joule

Persamaannya dapat ditulis:

Q =

U + ΔW

Kesimpulan : Bahwa tidak mungkin suatu mesin akan bekerja terus menerus tanpa penambahan energi dari luar (perpetum mobille I ).

ΔQ, ΔU dan ΔW harus dinyatakan dalam satuan yang sama: joule, atau ft lb atau kalori, atau Btu.

a. Proses Isobarik

Proses isobarik adalah suatu proses dimana pada proses tersebut tekanannya adalah tetap.

Diagram antara tekanan terhadap waktu seperti gambar di bawah ini.

Berdasarkan diagram tersebut di atas Usaha yang dilakukan gas adalah :

W = p(V2 – V1)

W = usaha yang dilakukan gas (J)

p = tekanan gas (Pa)

V1 = Volume gas pada keadaan awal (m3)

V2 = Volume gas pada keadaan akhir (m3)

Jika pada proses ekspansi, volume gas membesar maka dikatakan gas melakukan usaha, tetapi jika pada proses pemampatan, volume gas mengecil maka dikatakan gas dikenai kerja.

Proses isobarik adalah proses di mana tekanan sistem tidak berubah.

Qp = m cp

atau :

Qp = n cp

= P

V = n R

U =

Untuk gas monoatomik: ∆U = 3/2 N k

T = 3/2 n R

T = n cv

cv = 3/2 R joule/mol K

Qp =

U +

n cp

T = n cv

T + n R

cp = cv + R joule/mol K

sehingga cp = 3/2 R + R = 5/2 R joule/mol K

Untuk gas diatomik:

Suhu Rendah : cv = 3/2 R ; cp = 5/2 R

Suhu Sedang : cv = 5/2 R ; cp = 5/2 R

Suhu Tinggi : cv = 7/2 R ; cp = 7/2 R

1 J/mol K =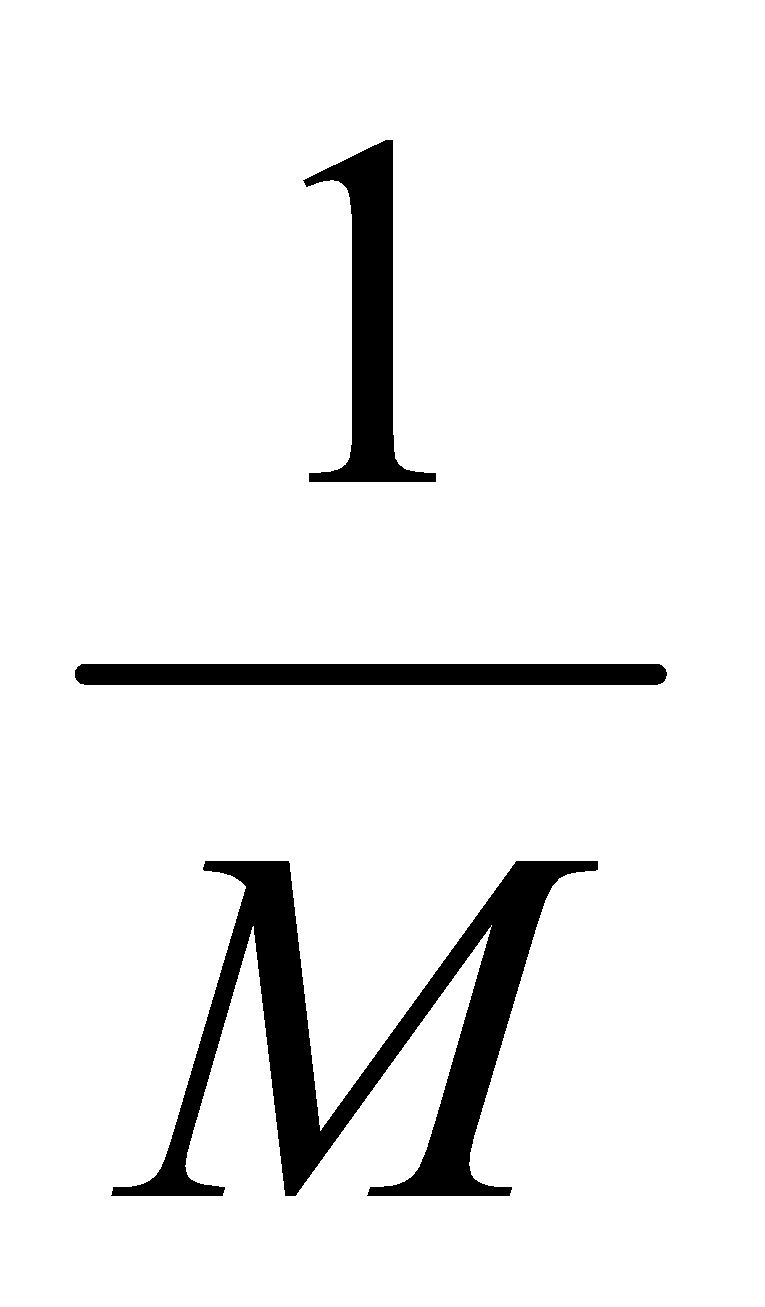

J/kg K

Gas Monoatomik : cv = 3/2 R/M

joule / kg K

cp = 5/2 R/M

b. Proses Isokhorik

Proses isokhorik adalah suatu proses dengan volume tetap di mana volume sistem tidak berubah, yakni kalor yang masuk sistem menjelma sebagai penambahan energi dalam sistem.

Pada proses volume tetap berlaku hukum Gay-Lussac yang menyatakan :

diagram hubungan antara tekanan dan volume adalah sebagai berikut :

V V

Usaha yang dilakukan gas pada proses isokhorik adalah sebagai berikut : pada proses isokhorik ∆ V = 0 maka usaha yang dilakukan gas yang mengalami proses ini memenuhi : ΔW = p ΔV = 0

sehingga hukum I termodinamika menjadi : ΔQ = ΔU +ΔW

W = 0 ( tidak terjadi perubahan volume)

Maka

Qv =

Qv = n cv

T atau

Qv = m cv

U = 3/2 nR T (gas monoatomik=gas diatomik suhu rendah)

U = 5/2 n R T (gas diatomatik suhu sedang )

U = 7/2 n R (gas diatomatik suhu tinggi)

W =Qp − Qv

W = n (cp−cv) T atau W = m(cp-cv) T

Kapasitas Kalor

Q = m c

disebut dengan C

C =

Gas diatomik

Suhu Rendah : cv = 3/2 R/M ; cv = 3/2 nR

: cp = 5/2 R/M ; cp = 5/2 n R

Suhu Sedang : cv = 5/2 R/M J/kg.K ; cv = 5/2 nR J/K

: cp = 7/2 R/M ; cp = 7/2 n R

Suhu Tinggi : cv = 7/2 R/M ; cv = 7/2 nR

: cp = 9/2 R/M ; cp = 9/2 n R

Gas monoatomik :

Qv =

T = 3/2 n R

Cv = 3/2 n R

c. _ Proses Isotermik

Proses isotermik adalah proses di mana suhu tidak berubah. Untuk gas ideal yang mengalami proses isotermik ΔU = 0. Tetapi hal ini tidaklah berlaku untuk sistem-sistem lain. Sebagai contoh kalau es mencair pada 0°C, ΔU ≠ 0 meskipun proses pencairan berlangsung pada suhu tetap.

Proses Isotermik gas ideal:

U = O

Q =

W = n RT 1n (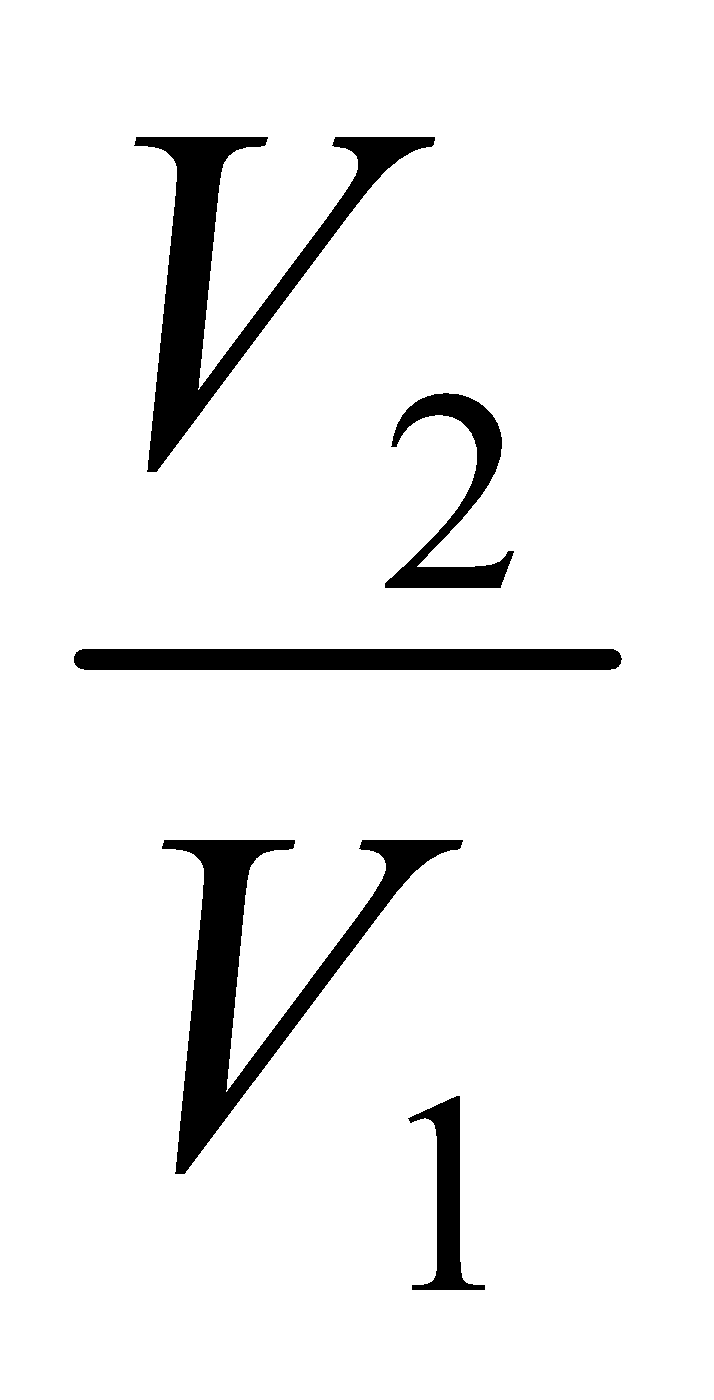

)

W = n RT 1n (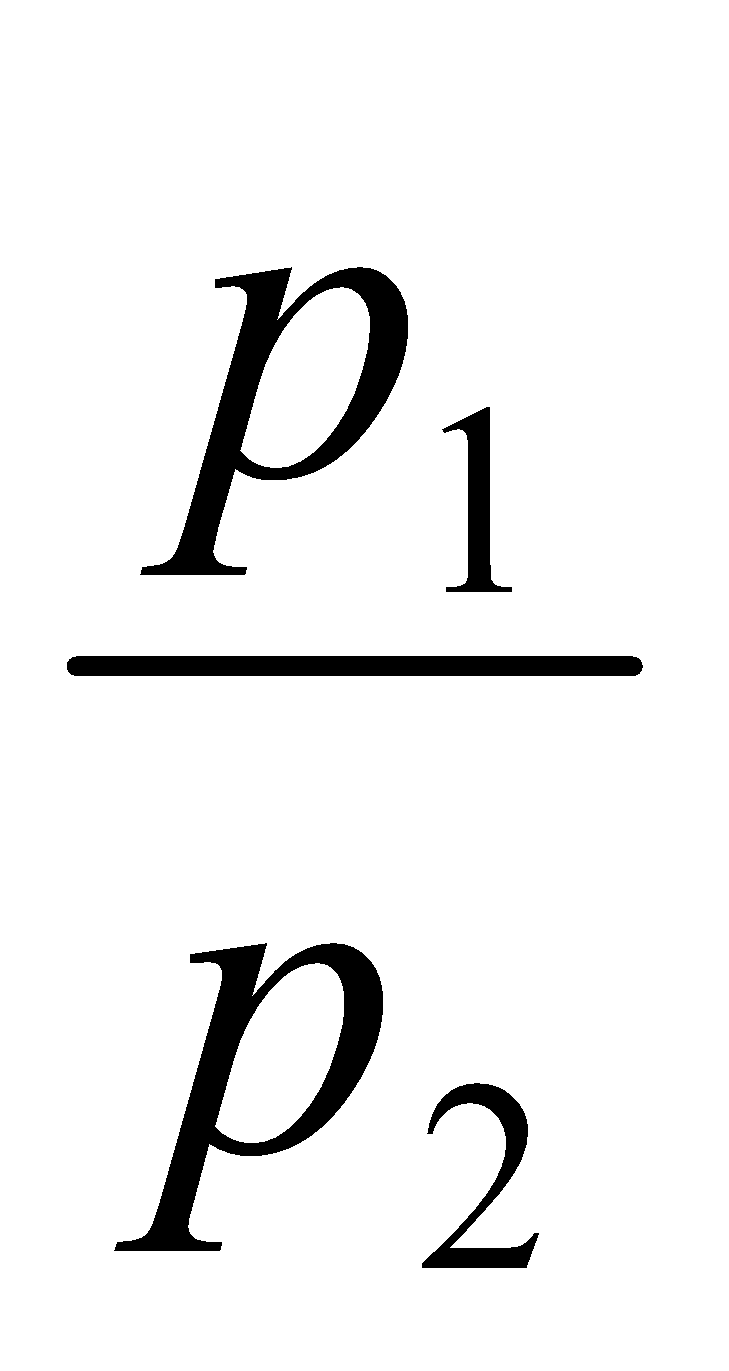

)

W = P

V = n R

Apabila gas ideal mengalami proses di mana (p1, V1) berubah menjadi (p2, V2), di mana p1 V1 = p2 V2 , berlaku bahwa:

ΔQ = ΔW = p1 V1 ln

= 2,30 p1 V1 log

Disini ln dan log adalah logaritma dengan bilangan dasar e dan 10.

d. _ Proses Adiabatik

Proses adiabatik adalah proses di mana tidak ada kalor yang masuk atau keluar dari sistem. Maka ΔQ = 0, hingga untuk proses demikian, hukum pertama menjadi :

0 = ΔU + ΔW

artinya

U = −

Apabila sistem melakukan kerja, energi dalamnya harus turun. Apabila kerja dilakukan pada sistem, energi dalamnya akan naik. Apabila gas ideal mengalami proses, di mana keadaannya (p1, V1, T1) berubah secara adiabatik menjadi (p2, V2, T2), berlakulah : p1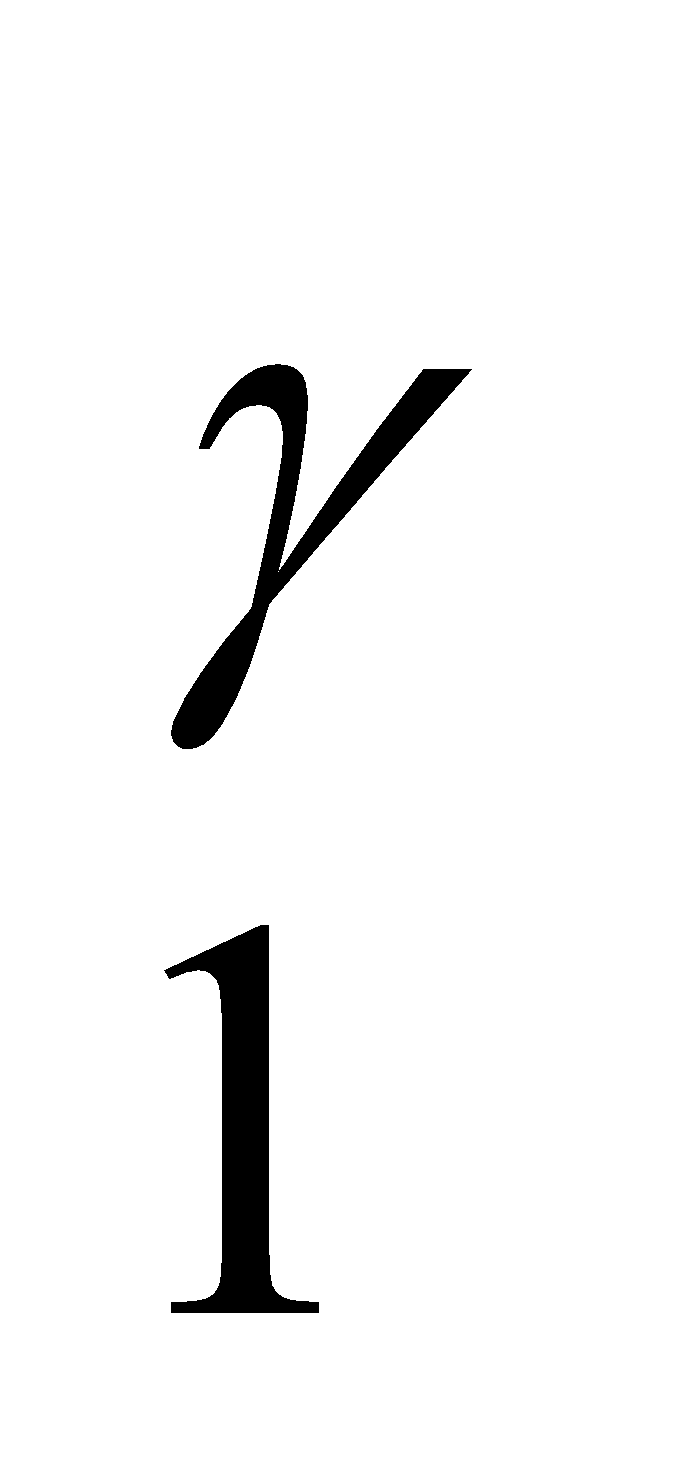V

= p2V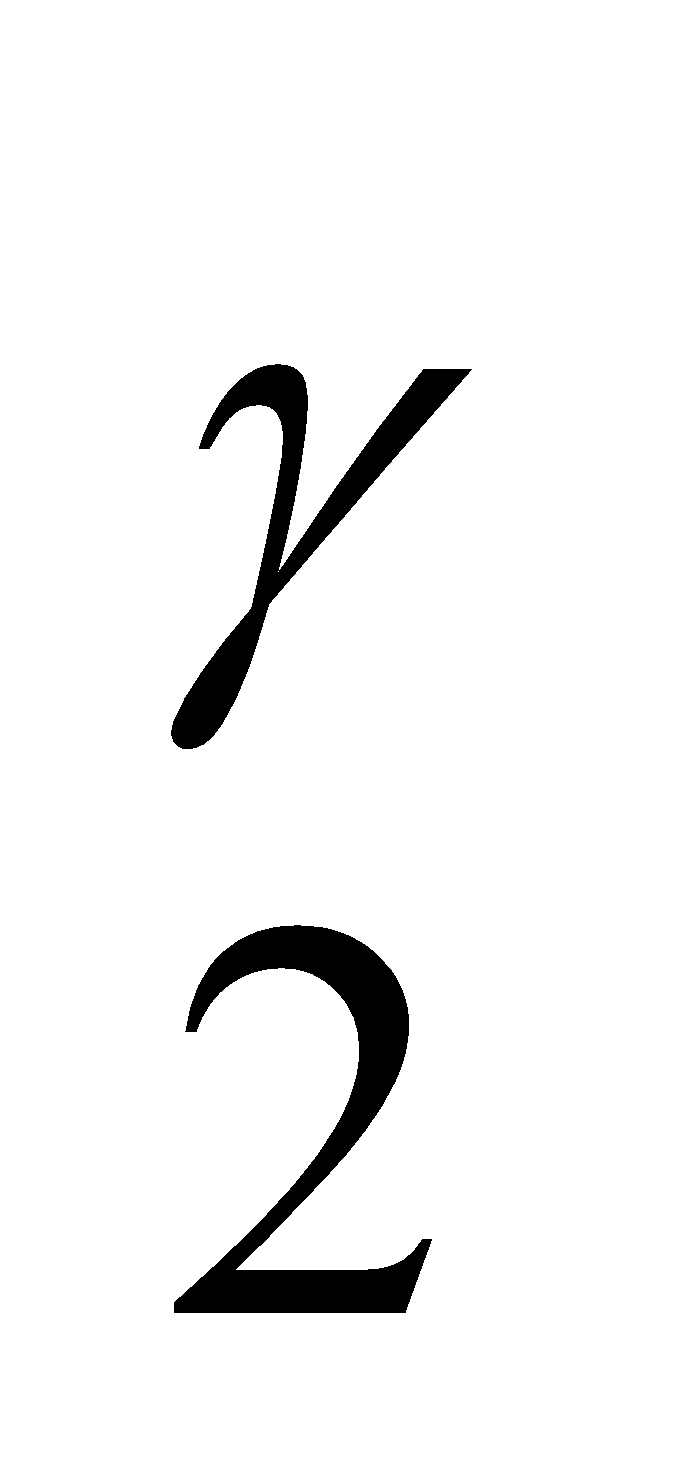

dan

dengan γ = cp/cv.

Pelaksanaan hukum I Termodinamika pada proses-proses di atas mengikuti hukum kekekalan energi.

C.TERMODINAMIKA 2

Hukum II termodinamika dirumuskan oleh beberapa ilmuan diantaranya sebagai berikut.

Rudolf Clausius :

Perumusan Clausius tentang hukum II Termodinamika secara sederhana dapat diungkapkan sebagai berikut : Tidak mungkin membuat mesin pendingin yang bekerjanya hanya menyerap dari reservoir bersuhu rendah dan memindahkan kalor itu ke reservoir yang bersuhu tinggi, tanpa disertai perubahan lain. kelvinClausius[1]

Dengan kata lain bahwa, kalor mengalir secara spontan dari benda bersuhu tinggi ke benda bersuhu rendah dan tidak secara spontan kalau kembali ke keadaan semula. Atau singkatnya W ≠ 0, bagi mesin pendingin.

Kelvin − Planck (Perpetom Mobiles II)

Pada dasarnya perumusan antara Kelvin dan Plank mengenai suatu hal yang sama, sehingga perumusan keduanya dapat digabungkan dan sering disebut : Perumusan Kelvin-Plank Tentang Hukum II Termodinamika.

Perumusan Kelvin-Plank secara sederhana dapat dinyatakan sebagai berikut : tidak mungkin membuat mesin yang bekerjanya semata-mata menyerap kalor dari sebuah reservoir dan mengubahnya menjadi usaha. Atau dengan kata lain bahwa, tidak mungkin suatu mesin itu mengisap panas dari reservoir dan mengubah seluruhnya menjadi usaha. Atau singkatnya Q1 ≠ 0, yaitu η < 1 bagi setiap mesin kalor.

Carnot

Dari semua mesin yang bekerja dengan menyerap kalor dari reservoir panas dan membuang kalor pada reservoir dingin efisiensinya tidak ada yang melebihi efisien mesin Carnot. Mesin Carnot secara ideal memang tidak ada, tetapi mesin yang mendekati mesin Carnot akan memiliki efisiensi yang tinggi, maksudnya dapat mengubah panas sebanyak- banyaknya menjadi energi gerak mekanik. Ciri khas mesin Carnot ialah pemanasan dan pendinginannya, yaitu pengisapan dan pelepasan panasnya berlangsung secara isotermis, sedangkan pengembangan dan penekanannya berlangsung secara adiabatis. Dengan demikian mesin Carnot dapat dibalik (reversible), karena proses isotermis maupun adiabatis selalu dapat dibalik, maksudnya dengan mengenakan usaha mekanik W padanya mesin akan melepas panas Q1 dari bagian yang didinginkan serta melepas panas sebanyak Q2 keluar. Jenis-jenis mesin selain mesin Carnot tidak dapat dibalik, dan dengan menerapkan hukum termodinamika ke II dapat ditunjukkan bahwa karena dapat dibalik, mesin Carnot memiliki efisiensi yang sama.

Hukum II termodinamika diringkaskan berbunyi sebagai berikut.

Adalah tidak mungkin mendapatkan suatu mesin yang bekerja dalam lingkaran yang tidak menimbulkan efek lain selain mengambil panas dari suatu sumber dan mengubah panas ini seluruhnya menjadi usaha. Hukum II termodinamika juga menyatakan bahwa panas tidak akan mengalir atau menghantar dari suhu rendah ke suhu tinggi, yang pasti adalah dari suhu tinggi ke suhu rendah.

Bab II.Penutup

A.Kelebihan dan Kekurangan

Pada Buku 1

1. memiliki pembahasan yang lebih sempurna,

2.dilengkapi dengan rumus-rumus yang lebih lengkap dan penggunaan tata bahasa yang mudah dimengerti sehingga para pembaca dapat dengan lebih mudah didalam mempelajari tentang Mekanika Fluida maupun Termodinamika pada buku tersebut.

3.Pada Buku 1 tersebut banyak cakupan materi pembelajaran tentang Mekanika Fluida dan Termodinamika yang tidak dijelaskan pada Buku 2 sehingga Buku 1 adalah buku yang lebih lengkap materi pembelajarannya,

4. juga dilengkapi dengan pendapat-pendapat para ahli sedangkan,

Pada Buku 2

masih memiliki banyak kekurangan diantaranya adalah penjelasan rumus-rumus atau penurunan rumus-rumus yang kurang lengkap dan masih banyak cakupan materi pembelajaran tentang Mekanika Fluida dan Termodinamika yang tidak dimuat dalam Buku 2 tersebut.

-sehingga buku yang lebih baik digunakan para pembaca didalam mempelajari Mekanika Fluida dan Termodinamika adalah Buku 1

B.Kesimpulan

Tiada satu pun teknik pembuatan bagan yang telah dikemukakan dalam uraian ini dengan sendirinya akan memberikan jawaban yang tepat tentang masalah metode kepada kita. Juga tiada satu pun yang dengan sendirinya akan menghasilkan suatu metode yang paling baik yang dapat kita pakai.

Teknik-teknik tersebut hanyalah menyajikan cara-cara penyusunan fakta- fakta mengenai sistem dalam bentuk yang sejelas-jelasnya dan mudah dimengerti. Kemudian, dengan mempergunakan akal sehat dan pengalaman masa lampau, dan dengan menerapkan prinsip-prinsip, disertai dengan mengajukan pertanyaan – pertanyaan kunci yang bersifat skeptis (yang meragu-ragukan), maka jalan untuk mengadakan perbaikan-perbaikan prosedur akan terbuka dengan sendirinya. Perbaikan-perbaikan itu tentu saja perlu di analisa secara kritis, sama halnya dengan sistem yang telah ada, agar perbaikan-perbaikan itu benar-benar bermanfaat.

Daftar pustaka

-Michael J. Moran, Howard N. Shapiro, Alih Bahasa

Yulianto sutyo nogroho.:Panas dan Termodinamika Teknik Jilid 1 Edisi 4,

Erlangga, 2004, (hal 92 – 155). Buku 1

-Purwoko-Fendi,2010,fisika,Yudhistira…BUKU 2

MAKALAH

MENU

Search This Blog

Labels

Sunday, 7 February 2016

CRITIKAL BOOK REPORT Tentang MEKANIKA FLUIDA dan TERMODINAMIKA

No comments:

Post a Comment

Pages

Pages

Pages

Pages